Eolymp 325: Dangerous route

Problem statement

In one country there are n cities, some of which are connected by two-way routes. Cities are numbered by integers from 1 to n. In times of financial crisis the level of the crime in a state rose and the crime groups are organized. The most dangerous of these was “Timur and his gang” led by a notorious criminal circles by Timur, that commit robberies on most of the roads. As a result, some roads became dangerous to drive.

Baha must get out of city 1 and go to city n. Since he appreciate his life too much (and his wallet also), he decided to cheat Timur and go to destination by the least dangerous route, even if it is not the shortest. Baha defined the level of the danger for each road as an integer from 0 (safe) to 10^6 (very dangerous). The danger of the route is the maximum value among the dangers of the roads that make up this route.

Help him to choose the safest route (one which has the minimum possible risk).

Input data

First line contains two integers n and m (2 ≤ n, m ≤ 10^6). Each of the next m lines defines one road and contains three integers:

• a, b (1 ≤ a, b ≤ n) - cities, connected with the road;

• c (0 ≤ c ≤ 10^6) - the danger of the road.

Any two cities can be connected by several roads.

Output data

One integer - the danger of the most safe route.

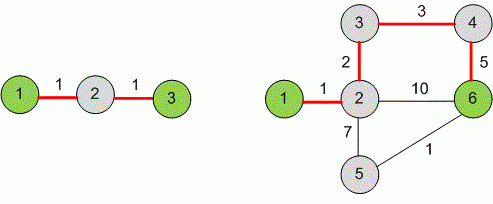
Examples

Solution

The first algorithm that can come to mind is to use DFS or BFS, however, in those algorithms, you would have a hard time to keep track of route (and the graph can be circular, which makes things harder) and the maximum danger in that route. As the problem implies, we need to take the least dangerous way, in which the least is defined by maximum danger on the trip. So, we can sort the nodes based on their danger level, and then traverse the nodes until we find our destination.

This type of problems is usually solved with disjoint set data structure. We are going to view each node as different set, and then, merge these sets, until we connect 1 to n. For each set, we are going to remember the parent/representative of each node in that set. In the beginning, each node is parent of itself.

int parent[MAX];

int repr(int node)
{
    if (node == parent[node]) return node;
    return parent[node] = repr(parent[node]);
}

This recursion sets the parent for each node in the disjoint set. When we merge two sets, we change second set’s node’s parents to the parent of the first set. So:

int unite(int x, int y)
{
    int repr1 = repr(x);
    int repr2 = repr(y);

    // sanity check, make sure you are not connecting already connected
    if (repr1 != repr2)
        parent[repr2] = repr1;

}

As stated above, we also need to sort the edges based on their danger levels. For this, we will use qsort with comparator. After sorting, we are going to merge disjoint sets, until nodes 1 and n are connected, that is, repr(1) = repr(n). So, the overall code looks like this:

#include <stdio.h>
#include <stdlib.h>

#define MAX 1000001

int parent[MAX];

typedef struct
{
    int x, y, danger;
} edge;

int repr(int node)
{
    if (node == parent[node])
        return node;

    return parent[node] = repr(parent[node]);
}

void unite(int x, int y)
{
    int x1 = repr(x);
    int y1 = repr(y);

    // sanity check, make sure you are not connecting already connected
    if (x1 != y1)
        parent[x1] = y1;
}

int comp(const void *e1, const void *e2)
{
    return ((edge *)e1)->danger - ((edge *)e2)->danger;
}

int main()
{
    edge edges[MAX];

    int n, m, i;
    scanf("%d %d", &n, &m);

    // In the beginning, each node is its parent
    for (i = 1; i <= n; ++i)
        parent[i] = i;

    for (i = 0; i < m; ++i)
        scanf("%d %d %d", &edges[i].x, &edges[i].y, &edges[i].danger);

    qsort(edges, m, sizeof(edge), comp); // sort by ascending danger

    for (i = 0; i < m; ++i)
    {
        unite(edges[i].x, edges[i].y);

        if (repr(1) == repr(n)) // update parents, and check if 1 and n is connected
            break;
    }

    printf("%d\n", edges[i].danger);

    return 0;
}

If we submit this code:

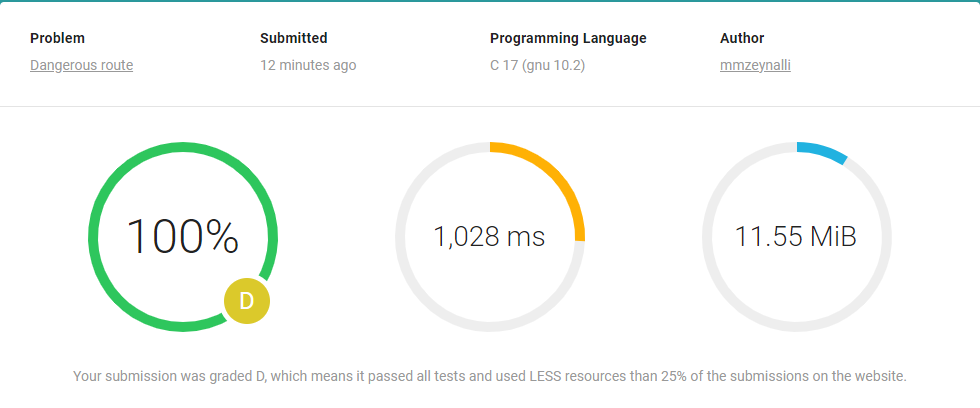
Hmmm… We got grade D, because we are using more resources? Maybe it is because we have static max size array, what if we do it dynamic, and give minimal size?

int *parent;

// Rest of the functions

int main()
{
    edge *edges;
    int n, m, i;
    scanf("%d %d", &n, &m);

    parent = (int *)malloc((n + 1) * sizeof(int));
    edges = (edge *)malloc(m * sizeof(edge));

    // Rest of the code

    free(parent);
    free(edges);
}

AND THE EXPECTED RESULT IS:

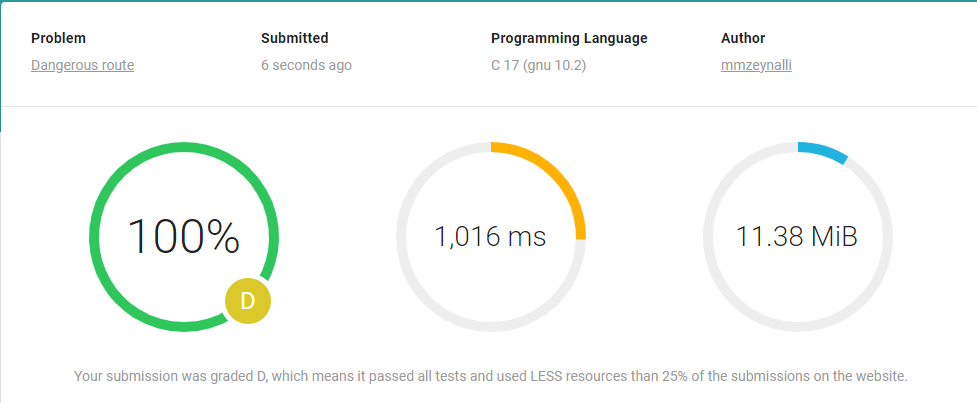
What, the same?? Hold on a minute. What is the problem then?

Maybe, let’s try to write this code in C++:

#include <bits/stdc++.h>
#define MAX 1000001

using namespace std;

struct edge
{
    int x, y, danger;
} edges[MAX];

vector<int> parent;

int repr(int node)
{
    if (node == parent[node])
        return node;

    return parent[node] = repr(parent[node]);
}

void unite(int x, int y)
{
    int x1 = repr(x);
    int y1 = repr(y);

    if (x1 != y1)
        parent[x1] = y1;
}

int f(edge a, edge b)
{
    return a.danger < b.danger;
}

int main()
{
    int n, m, i;
    scanf("%d %d", &n, &m);

    parent.resize(n + 1);

    for (i = 1; i <= n; i++)
        parent[i] = i;

    for (i = 0; i < m; i++)
        scanf("%d %d %d", &edges[i].x, &edges[i].y, &edges[i].danger);

    sort(edges, edges + m, f);

    for (i = 0; i < m; i++)
    {
        unite(edges[i].x, edges[i].y);

        if (repr(1) == repr(n))
            break;
    }

    printf("%d\n", edges[i].danger);
    return 0;
}

What if we submit this?

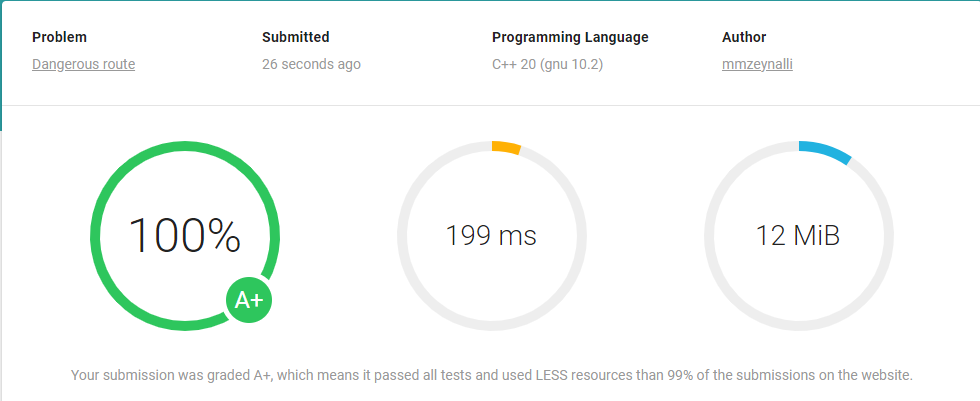
Wow, A+? So, what is the difference? Is it because of we used vector?

Appears no. I also found out while solving this problem. According to Scott Meyers, in his Effective STL book - item 46, std::sort is about 670% faster than qsort due to the fact of inline. 670% Carl, 670%!

Anyways, we managed to score A+! Yay! You can access the code here. Feel free to contribute your solution in different language!